Infinite asymptotics
Big O notation is useful when analyzing algorithms for efficiency. For example, the time (or the number of steps) it takes to complete a problem of size n might be found to be T(n) = 4n2 − 2n + 2.
As n grows large, the n2 term will come to dominate, so that all other terms can be neglected — for instance when n = 500, the term 4n2 is 1000 times as large as the 2n term. Ignoring the latter would have negligible effect on the expression's value for most purposes.
Further, the coefficients become irrelevant if we compare to any other order of expression, such as an expression containing a term n3 or n4. Even if T(n) = 1,000,000n2, if U(n) = n3, the latter will always exceed the former once n grows larger than 1,000,000 (T(1,000,000) = 1,000,0003= U(1,000,000)). Additionally, the number of steps depends on the details of the machine model on which the algorithm runs, but different types of machines typically vary by only a constant factor in the number of steps needed to execute an algorithm.
So the big O notation captures what remains: we write either
or
and say that the algorithm has order of n2 time complexity.
Note that "=" is not meant to express "is equal to" in its normal mathematical sense, but rather a more colloquial "is", so the second expression is technically accurate (see the "Equals sign" discussion below) while the first is a common abuse of notation.[1]
[edit]Infinitesimal asymptotics
Big O can also be used to describe the error term in an approximation to a mathematical function. The most significant terms are written explicitly, and then the least-significant terms are summarized in a single big O term. For example,
expresses the fact that the error, the difference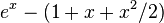 
, is smaller in absolute value than some constant times | x3 |when x is close enough to 0.
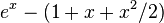, is smaller in absolute value than some constant times | x3 |when x is close enough to 0.
